简介

并查集是一种树状结构，主要用于处理集合的合并和查找问题，其能在较低的时间复杂度内完成对集合元素的判断，常用于判断某些元素是否属于同个集合。

数据结构

并查集是一种树状结构，但是跟一般的树形结构不太一样。平常的树结构主要是从上往下进行查找，所以数据结构中也经常有用于表示左右孩子的指针，但是并查集主要是从下往上进行查找，并不需要从上往下的查找，所以在并查集中并没有左右孩子的指针，取而代之的是用于表示当前节点的父节点的数组（当节点简单可以用数组下标表示所有节点时）或 map （当节点比较复杂，无法用数组的下标表示所有节点时，用 map 结构来表示节点的父节点）

算法

并查集的主要操作有三个：初始化、查找、合并。

初始化

初始化，是设置每个节点的父节点为自己的本身（当然，为了方便计算，也可以设置成其他值，如 0 或 null）。代码如下

for (int i = 0; i < parents.length; i++)
{
    parents[i] = i;
}

查找

查找，主要是根据输入的节点依次遍历查找其父节点，知道找到当前分支的根节点为止。这是判断两个节点是否属于同个集合的关键所在。查找的过程是一个递归的过程。其代码如下

// 递推版
int find(int[] parents, int i)
{
    int current = i;
    while (parents[current] != current)
    {
        current = parents[current];
	}
    
    return current;
}

// 递归版
int find(int[] parents, int i)
{
    if (i == parents[i])
    {
        return i;
	}
    
    return find(parents, parents[i]);
}

路径压缩

普通的查找是循着路径一层层向上查找，如果树的深度过大，每次都沿着底层向上查找会变得很慢，如果在查找的过程中，将查找路径上的节点都直接指向根节点，则下次再查找路径上的节点时，就能直接获取到结果，而不用遍历查找了，这样就能提高查找速度。这就是路径压缩。其效果如下图所示：

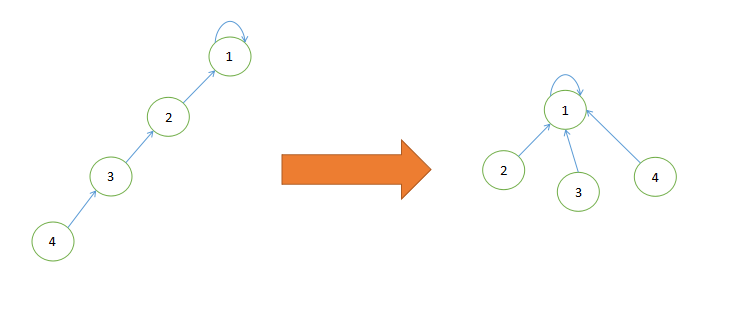
代码如下：

int find(int[] parents, int i)
{
    if (i == parents[i])
    {
        return i;
    }
    
    int root = find(parents, parents[i]);
    parents[i] = root;
    return root;
}

合并

在构建集合的过程中，如果已经明确两个元素属于同一个集合，当时当前这两个元素的根节点并不相同，那么就要将这两个元素的根节点进行关联，这就是合并操作，其主要动作是将某个节点的父节点指向另一个根节点，至于哪个根节点作为父节点，这个可以自己根据规则进行定义，一般情况下，无特殊要求，也可以随机指定。代码如下

void union(int i, int j, int[] parents)
{
    int iParent = parents[i];
    int jParent = parents[j];
    if (iParent != jParent)
    {
        parents[iParent] = jParent;
    }
}

带权并查集

上述的并查集，只是一种简单的判断元素是否在集合中，对于一些稍微复杂一点的情况，如两点之间的距离，就需要在边上记录额外的信息，在查找和合并的同时也需要进行对应边的值的更新操作，这样才能保证最终结果的正确性。

假设用 values[i] 表示当前节点到父节点的路径（边的值），在查找过程的路径压缩过程中，需要实时更新边值，其代码如下：

int find(int[] parents, int i, int[] values)
{
    if (i == parents[i])
    {
        return i;
    }
    
    // 找到根节点
    int root = find(parents, parents[i], values);
    
    // 更新边的值，这是递归的返回动作，必须在路径压缩前，这样才能保证值的准确性
    values[i] = values[parents[i]] + values[i];
    
    // 路径压缩
    parents[i] = root;
    
    return root;
}

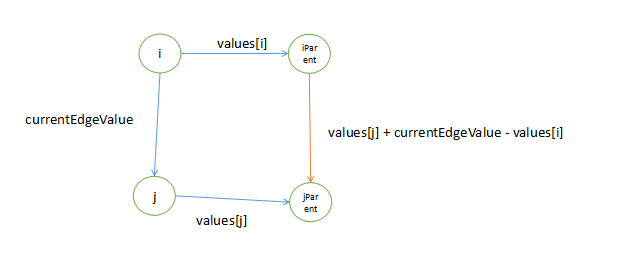
关于合并操作，由于需要把某个节点的根节点指向另一个根节点（即：将某个根节点变成其他节点的子节点），此时需要更新变动的根节点的边值（不再指向自己，而是执行其他节点，边值从 0 值（广义的 0 值，并不是真正的数字 0，其具体值根据题目不同而不同） 变成 非 0 值）。其代码如下

void union(int i, int j, int[] parents, int[] values, int currentEdgeValue)
{
    int iParent = parents[i];
    int jParent = parents[j];
    if (iParent != jParent)
    {
        parents[iParent] = jParent;
        // currentEdgeValue 是 i 到 j 的边的值
        values[iParent] = currentEdgeValue + values[j] - values[i]
    }
}