morris 算法

简介

morris 算法是一种二叉树的遍历算法，其利用树叶子节点的孩子为空的特点，将空的孩子节点临时指向其后继节点，后续再次遍历到该节点时重置为空使其恢复树的结构。这种遍历算法能够压缩空间，使其在 O(1) 的空间复杂度内完成对树结构的遍历。

算法主要过程

从根节点触发，对每个节点执行以下步骤

• 如果存在左孩子，则找出左孩子的最右节点，
  • 如果该节点为空，则将其右指针指向当前节点（这是第一次遍历到该节点），将当前指针移到左孩子上
  • 如果该节点指向了当前节点，则将其右指针置为空，恢复树的结构（这是第二次遍历到该节点），将当前指针移到右孩子上
• 如果不存在左孩子，则将当前指针移到右孩子上，进行下一轮遍历

通过上述遍历过程，如果某个节点有左孩子，则该节点被访问两次，如果节点没有左孩子，则该节点只被访问一次，因此，上述的遍历过程时间复杂度为 O(n)。由于使用循环遍历，没有使用递归的方式，因此不会有额外的空间消耗，其空间复杂度为 O(1)。

下面用一个例子来说明 morris 算法的遍历过程，假设有以下一颗树：

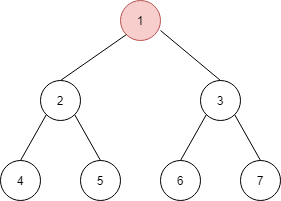
首先，指针在节点1 处，由于有左孩子 2 ，所以找到 2 的最右节点 5，由于节点 5 的右孩子为空，因此将其指向节点 1，并将当前指针移到左孩子节点 2 上。如下图所示

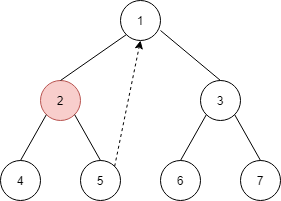
接着，由于节点 2 有左孩子 4，所以找到 4 的最右节点是它本身，由于节点 4 的右孩子为空，因此将其指向节点 2，并将当前指针移到左孩子节点 4 上。如下图所示

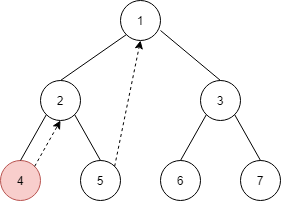
接着，节点 4 没有左孩子，直接到右孩子上（上一步骤已经将节点 4 的右孩子指向节点 2）上

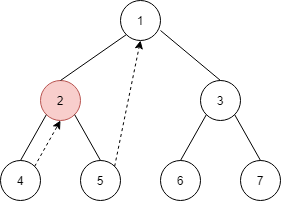
由于节点 2 有左孩子 4，所以找到 4 的最右节点是它本身，由于节点 4 的右孩子指向了当前节点，所以将节点 4 的右孩子节点置为空（还原树的结构），然后将当前指针移到右节点 5 上

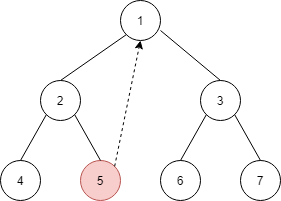
节点 5 没有左孩子，直接到右孩子上（之前步骤已经将节点 5 的右孩子指向节点 1）上

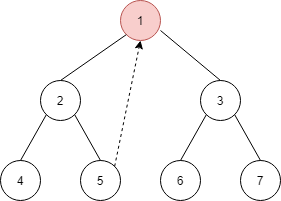
由于节点 1 有左孩子 2 ，所以找到 2 的最右节点 5，由于节点 5 的右孩子指向了当前节点 1，所以将节点 5 的右孩子置空（还原树的结构），然后将当前指针移到右节点 3 上

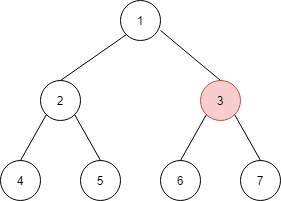
由于节点 3 有左孩子 6，所以找到 6 的最右节点是它本身，由于节点 6 的右孩子为空，因此将其指向节点 3，并将当前指针移到左孩子节点 6 上

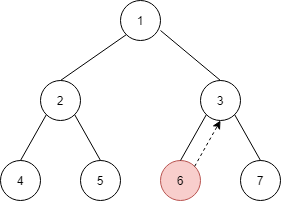
节点 6 没有左孩子，直接到右孩子上（上一步骤已经将节点 6 的右孩子指向节点 3）上

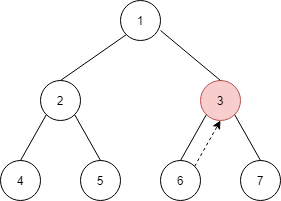
由于节点 3 有左孩子 6，所以找到 6 的最右节点是它本身，由于节点 6 的右孩子指向了当前节点，所以将节点 6 的右孩子节点置为空（还原树的结构），然后将当前指针移到右节点 7 上

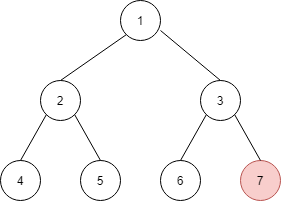
由于节点 7 的左右孩子都是空的，因此遍历结束。

前序遍历

使用 morris 算法可以在 O(1) 的空间复杂度和 O(n) 的时间复杂度下完成对树的前序遍历，而使用递归的方式，则需要 O(H)（树的高度，函数递归栈）的空间复杂度和 O(n) 的时间复杂度。一般情况下，都是使用递归的方式进行前序遍历（简单直观），如下所示

private void preOrderTraversal(TreeNode root)
{
    if (root == null)
    {
        return;
    }

    visit(root);
    preOrderTraversal(root.left);
    preOrderTraversal(root.right);
}

而如果对空间复杂度有特殊的要求，则可以使用 morris 算法来完成树的前序遍历，代码如下

private void preOrderMorrisTraversal(TreeNode root)
{
    TreeNode prev;
    TreeNode current = root;
    while (current != null)
    {
        if (current.left != null)
        {
            prev = current.left;
            while (prev.right != null && prev.right != current)
            {
                prev = prev.right;
            }

            if (prev.right == null)
            {
                prev.right = current;
                // 前序遍历，先访问节点，再访问左右子树，所以在第一次找左子树最右节点后，将访问根节点
                // 第二次找当前节点左子树最右节点后，不再重新访问
                visit(current);
                current = current.left;
            }
            else
            {
                prev.right = null;
                current = current.right;
            }
        }
        else
        {
            visit(current);
            current = current.right;
        }
    }
}

中序遍历

递归的中序遍历也很简单直观，代码如下

private void inOrderTraversal(TreeNode root)
{
    if (root == null)
    {
        return;
    }

    inOrderTraversal(root.left);
    visit(root);
    inOrderTraversal(root.right);
}

morris 的中序遍历跟前序遍历差不多，唯一不同就是访问根节点的顺序不同，前置遍历将访问根节点放在了第一次找根节点左子树最右节点的时候，中序遍历将访问根节点放在了第二次找根节点左子树最右节点的时候。

private void inOrderMorrisTraversal(TreeNode root)
{
    TreeNode prev;
    TreeNode current = root;
    while (current != null)
    {
        if (current.left != null)
        {
            prev = current.left;
            while (prev.right != null && prev.right != current)
            {
                prev = prev.right;
            }

            if (prev.right == null)
            {
                prev.right = current;
                current = current.left;
            }
            else
            {
                // 当前序节点右指针指向当前节点时，说明左子树已经遍历完成
                prev.right = null;
                // 中序遍历，需要先访问完左子树，再访问根节点
                // 所以需要在第二次找左子树的最右节点后才进行根节点的访问
                visit(current);
                current = current.right;
            }
        }
        else
        {
            visit(current);
            current = current.right;
        }
    }
}

后序遍历

递归的后续遍历，仍然是简单直观的

private void postOrderTraversal(TreeNode root)
{
    if (root == null)
    {
        return;
    }

    postOrderTraversal(root.left);
    postOrderTraversal(root.right);
    visit(root);
}

但 morris 的后序遍历就稍微复杂了点，其需要在第二次找根节点左孩子的最右节点时，以根节点左孩子到这个最右节点之间构成的链表进行反向遍历，完成树的后续遍历操作。

private void postOrderMorrisTraversal(TreeNode root)
{
    TreeNode prev;
    // 为方便操作，此处虚拟一个额外的根节点，让其左指针指向当前树的根节点
    // 并以这个虚拟根节点作为 morris 算法遍历开始的根节点
    TreeNode dummy = new TreeNode(DUMMY_VALUE);
    dummy.left = root;
    TreeNode current = dummy;
    while (current != null)
    {
        if (current.left != null)
        {
            prev = current.left;
            while (prev.right != null && prev.right != current)
            {
                prev = prev.right;
            }

            if (prev.right == null)
            {
                prev.right = current;
                current = current.left;
            }
            else
            {
                prev.right = null;
                // 此处以当前节点的左子树为链表头节点，每个节点的右节点相互连接构成一个链表
                // 对链表进行反向遍历访问，即可完成当前节点左子树的前序遍历
                visitReverse(current.left);
                current = current.right;
            }
        }
        else
        {
            // 和前序遍历和中序遍历不同，此处不会进行节点的访问
            // 因为后序遍历需要先遍历完左右子树才访问根节点
            // 如果此处直接访问节点，此时右子树并没有遍历完成，会造成错误
            current = current.right;
        }
    }
}

private void visitReverse(TreeNode root)
{
    TreeNode head = rightReverse(root);
    TreeNode current = head;
    while (current != null)
    {
        visit(current);
        current = current.right;
    }
    rightReverse(head);
}

// O(1) 空间复杂度、O(n) 时间复杂度进行链表倒序
private TreeNode rightReverse(TreeNode root)
{
    TreeNode head = root;
    while (root.right != null)
    {
        TreeNode next = root.right;
        root.right = next.right;
        next.right = head;
        head = next;
    }

    return head;
}

参考资料

[1] 风之筝.经典算法小评(2)——Morris树遍历算法 [J/OL]. https://ghh3809.github.io/2018/08/06/morris-traversal/#morris%E9%81%8D%E5%8E%86, 2018-08-06
[2] god-jiang. 神级遍历——morris[J/OL]. https://zhuanlan.zhihu.com/p/101321696, 2020-01-06