ChunNote
0%

leetCode-375:Guess Number Higher or Lower II

发表于 分类于

问题描述

给定一个正整数 n， 要求在范围 1~n 内找到预设的数字。每次猜测时都会得到比较结果，告知是猜中了还是比预设的数字大或小，如果猜中则赢得游戏，否则扣除猜测数字相同的金币数量，游戏过程中如果金币数量小于等于0，则输掉游戏。要求找到最小的金币数量，使得一定可以赢得游戏。题目链接：点我

样例输入输出

输入：n = 10
输出：16
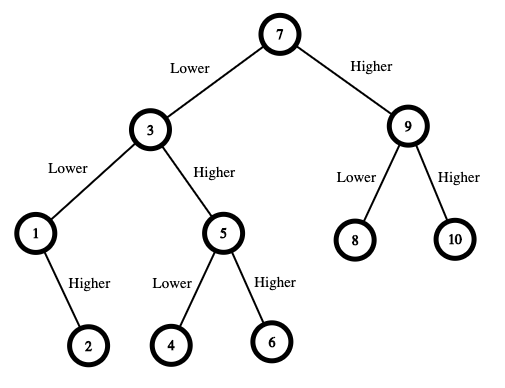
解释：制胜策略如下：

  • 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
    - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
    - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
    我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
    - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
    - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
    更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
    - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
    更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
    - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
    更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
    在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

输入：n = 1

输出：0

解释：只有一个数字，一猜即中

问题解法

采用记忆化搜索进行求解，用 dp[i][j] 表示 i ~ j 区间要赢得游戏所需的最小金币数量，则动态转移方程为 dp[i][j] = k + max(dp[i][k - 1], dp[k + 1][j])，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int getMoneyAmount(int n) {
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 0; i < n + 1; i++) {
            for (int j = 0; j < n + 1; j++) {
                if (i == j) {
                    dp[i][j] = 0;
                } else if (i + 1 == j) {
                    dp[i][j] = i;
                } else {
                    dp[i][j] = -1;
                }
            }
        }
        
        return search(dp, 1, n);
    }
    
    private int search(int[][] dp, int from, int to) {
        if (dp[from][to] != -1) {
            return dp[from][to];
        }
        
        int temp = Integer.MAX_VALUE;
        for (int k = from + 1; k < to; k++) {
            temp = Math.min(temp, k + Math.max(search(dp, from, k - 1), search(dp, k + 1, to)));
        }
        dp[from][to] = temp;
        
        return dp[from][to];
    }
}