ChunNote
0%

leetCode-304:Range Sum Query 2D - Immutable

发表于 更新于 分类于

问题描述

给定一个二维整形数组，要求多次查询某个子矩阵的和。题目链接：**点我**

样例输入输出

输入：

[“NumMatrix”, “sumRegion”, “sumRegion”, “sumRegion”]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]

输出：

[null, 8, 11, 12]

解释：

sample-picture

NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
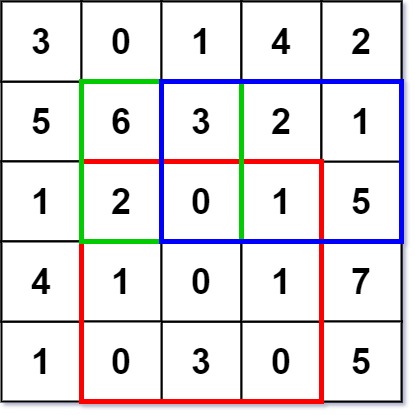
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

问题解法

此题最直接的做法就是每次查询都遍历子矩阵的值进行累加，不过这对单次查询是有效的，但是对于多次查询这效率就有点低，所以高效一点的做法是使用前缀和的思路，先对矩阵进行求和。用 dp[i][j] 表示从矩阵的左顶点到 (i, j) 节点的子矩阵的元素和。则 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j -1] + matrix[i][j]。对于求解 (row1, col1) 到 (row2, col2) 的子矩阵的元素之和，其结果可以用 dp[row2][col2] - dp[row2][col1 - 1] - dp[row1 - 1][col2] + dp[row1 - 1][col1 - 1] 来表示。这样，多次查询的时间复杂度就控制在 O(1) 内，只需要在开始的地方用 O(n * n) 的时间复杂度构造 dp 数组即可。代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class NumMatrix {
    int[][] matrixSum;

    public NumMatrix(int[][] matrix) {
        matrixSum = new int[matrix.length][matrix[0].length];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                matrixSum[i][j] = matrix[i][j];
                if (i > 0) {
                    matrixSum[i][j] += matrixSum[i - 1][j];
                }

                if (j > 0) {
                    matrixSum[i][j] += matrixSum[i][j - 1];
                }

                if (i > 0 && j > 0) {
                    matrixSum[i][j] -= matrixSum[i - 1][j - 1];
                }
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int result = matrixSum[row2][col2];

        if (row1 > 0) {
            result -= matrixSum[row1 - 1][col2];
        }

        if (col1 > 0) {
            result -= matrixSum[row2][col1 - 1];
        }

        if (row1 > 0 && col1 > 0) {
            result += matrixSum[row1 - 1][col1 - 1];
        }

        return result;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */