问题描述
给定一个二维数组,表示一组建筑的坐标,每个一维数组元素都是一个包含 3 个元素的数组,分别表示建筑的左坐标、建筑的右坐标、建筑的高度。要求列出这群建筑的 “天际线”。
天际线 应该表示为由 “关键点” 组成的列表,格式 [[x1,y1],[x2,y2],…] ,并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,y 坐标始终为 0 ,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
题目链接:**点我**
样例输入输出
输入:[[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出:[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释: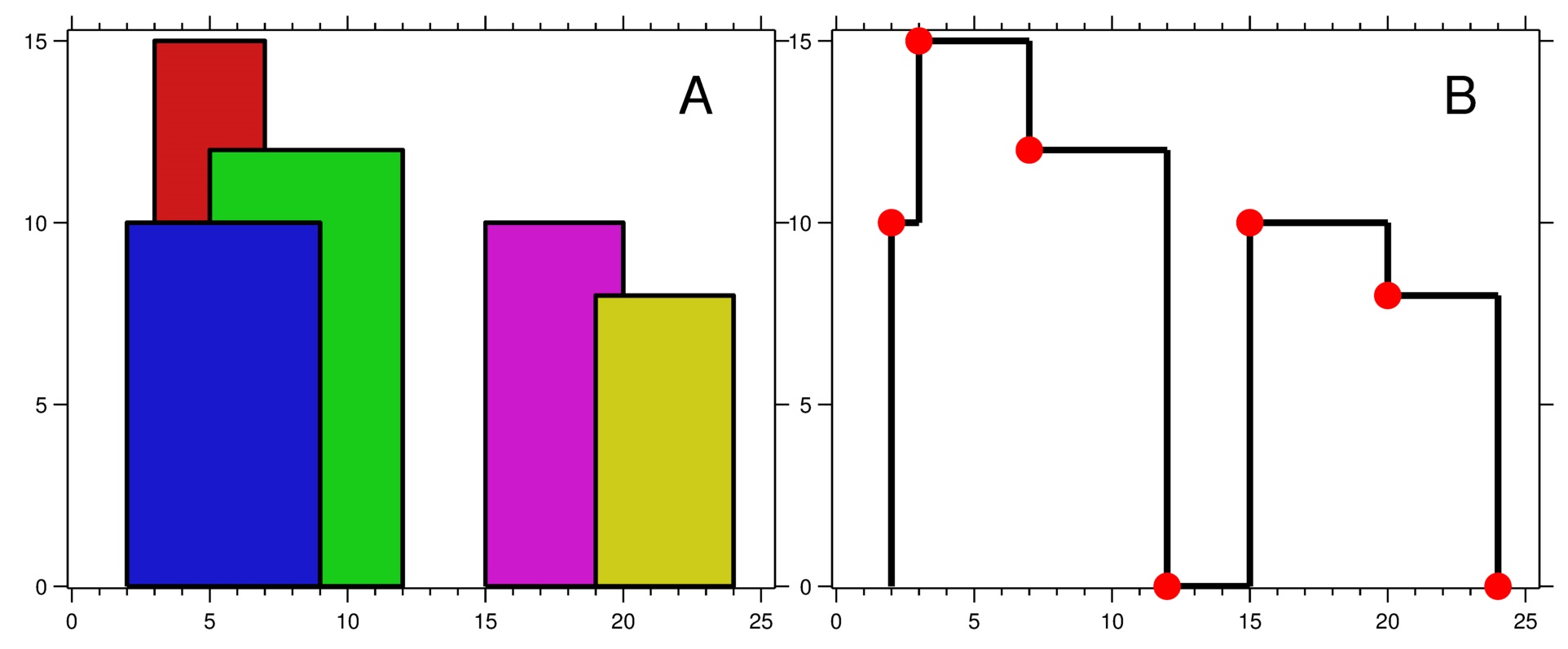
输入:[[0,2,3],[2,5,3]]
输出:[[0,3],[5,0]]
问题解法
此题主要参考:https://leetcode.cn/problems/the-skyline-problem/solution/gong-shui-san-xie-sao-miao-xian-suan-fa-0z6xc/。主要做法是先将建筑物的的端点进行排序(先按横坐标排序,如果横坐标相等,则按高度进行排序。如果高度也相等,则将右边建筑的左边界排在左边建筑的右边界前面),然后运用优先度列,遍历上述排序后的数组,如果是建筑的左边界,则加入队列中,如果是建筑的右边界,则从队列中移除。然后取出队列的最大值和当前高度进行比较,如果不一致,则说明这是一个边界点,需要记录。代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> lines = new ArrayList<>();
for (int[] building : buildings) {
List<Integer> left = new ArrayList<>();
left.add(building[0]);
left.add(-building[2]);
lines.add(left);
List<Integer> right = new ArrayList<>();
right.add(building[1]);
right.add(building[2]);
lines.add(right);
}
lines.sort((first, second) -> {
if (first.get(0).equals(second.get(0))) {
return first.get(1) - second.get(1);
}
return first.get(0) - second.get(0);
});
List<List<Integer>> result = new ArrayList<>();
PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());
queue.add(0);
int tempHeight = 0;
for (List<Integer> line : lines) {
if (line.get(1) < 0) {
queue.add(-line.get(1));
} else {
queue.remove(line.get(1));
}
int currentHeight = queue.peek();
if (currentHeight != tempHeight) {
tempHeight = currentHeight;
result.add(Arrays.asList(line.get(0), currentHeight));
}
}
return result;
}
}
|
参考资料
https://leetcode.cn/problems/the-skyline-problem/solution/gong-shui-san-xie-sao-miao-xian-suan-fa-0z6xc/
