简介
树状数组又叫二叉索引树(binary indexed tree),是一种用数组来表示“树”形状的数据结构,这里的“树”并不是真正意义上的树,是一个抽象意义上的“树”,其部分节点并不真实存在,只是为了方便理解而将其用“树”来表示。树状数组常用于求解动态数组(数组中的值经常发生变化)中的区间和。
算法
一般情况下,画二叉树都会将父节点放在左右子节点的中间,对于树状数组,将父节点位置调整到右子节点的方向上,如下图所示。
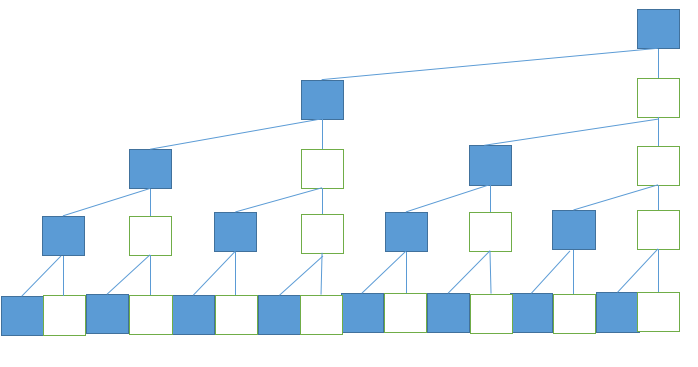
然后将树中白色背景的节点删除(算法过程中并不需要这部分节点),将蓝色背景的节点统一放到一个水平线上,就可以得到一个数组,如下图所示
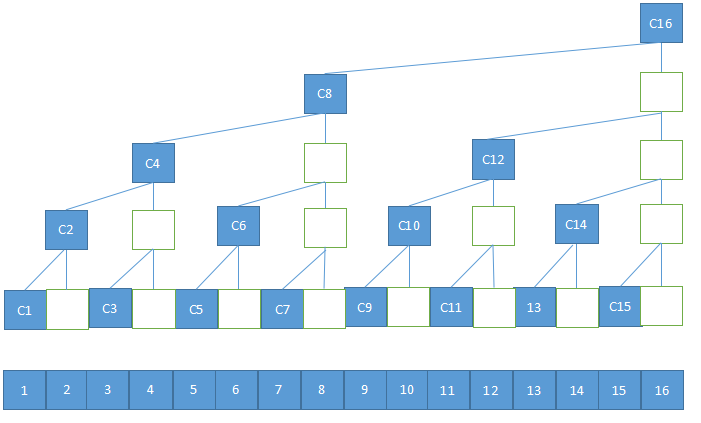
基于此,就可以用一个数组来表示存储一颗“树”,并用这颗“树”来执行相关业务计算,比如区间和。
但是,对于一个原始数组,怎么将其表示成树状数组呢。首先,要引入一个 lowbit 的概念,lowbit(n) 表示正整数 n 的二进制数的最低位 1 的位置对应数(整数二进制 32 位数里,只在这个位置有数 1,其他位置均为 0)。比如 6 的二进制数是 110,则 lowbit(6) = 2,5 的二进制数为 101,则 lowbit(5) = 1,8 的二进制数为 1000, 则 lowbit(8) = 16。关于 lowbit 有个快速的计算方法: lowbit(n) = n & (-n)。
知道了 lowbit 的含义,现在来构建树状数组。假设用 C 数组来表示构建的树状数组,C[n] 表示 n 节点或左右子树节点之和(如果存在左右子树的话),对于叶子节点,会自动对应到原始数组中。从下图中可以看出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| C[1] = nums[1]
C[2] = C[1] + nums[2] = nums[1] + nums[2]
C[3] = nums[3]
C[4] = C[2] + C[3] + nums[4] = nums[1] + nums[2] + nums[3] + nums[4]
C[5] = nums[5]
C[6] = C[5] + nums[6] = nums[5] + nums[6]
C[7] = nums[7]
C[8] = C[4] + C[6] + C[7] + nums[8] = nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6] + nums[7] + nums[8]
C[9] = nums[9]
C[10] = C[9] + nums[10] = nums[9] + nums[10]
C[11] = nums[11]
C[12] = C[10] + nums[11] + nums[12] = nums[9] + nums[10] + nums[11] + nums[12]
C[13] = nums[13]
C[14] = C[13] + nums[14] = nums[13] + nums[14]
C[15] = nums[15]
C[16] = C[8] + C[12] + C[14] + C[15] + nums[16] = nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6] + nums[7] + nums[8] + nums[9] + nums[10] + nums[11] + nums[12] + nums[13] + nums[14] + nums[15] + nums[16]
|
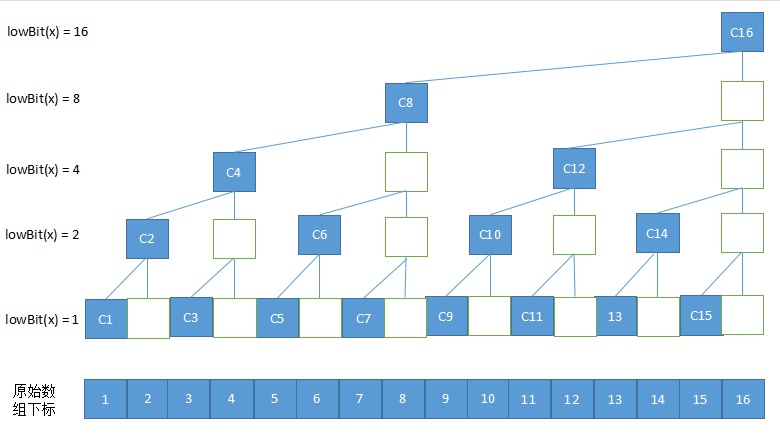
从上述的数组等式中,可以看出,树状数组中的元素包含了原始数组中的部分元素。当初始数组的某个元素发生变化时,树状数组中的部分元素需要跟着改变(树状数组的元素构成里包含了初始数组的这个元素)。比如改变 nums[1] 时,C[1]、C[2]、C[4]、C[8]、C[16]都会发生改变,改变 nums[7] 时, C[7]、C[8]、C[16] 会跟着改变,改变 nums[16] 时,只有 C[16] 会发生变化。
那当某个值发生变化时,怎么知道有哪些值会受影响呢。这里有个递归公式可以判断:当树状数组中 i 的位置发生变化时, i + lowbit(i) 的位置也会发生变化。所以可以得出以下的代码
1
2
3
4
5
6
7
8
9
10
|
public void update(int index, int val) {
int increaseNum = val - nums[index];
nums[index] = val;
for (int i = index; i < sums.length; i += lowBit(i)) {
sums[i] += increaseNum;
}
}
|
上述的代码虽然是对数组的更新操作,但是同样可以用在构建树状数组的过程中。因为构建树状数组的过程可以看做是将一个初始数组元素都是 0 的数组更新成目标数组的元素的过程。因此,构建树状数组的代码可以是以下操作
1
2
3
4
5
6
|
int[] sums = new int[nums.length];
for (int i = 1; i < nums.length; i++) {
update(i, nums[i]);
}
|
说完了更新操作,接下来看查询操作。由于树状数组中的元素包含了部分初始数组的元素,因此,当查询初始数组的前缀和或区间和时,可以利用树状数组来快速求解。当求初始数组某个位置的前缀和时,可以利用递推公式在树状数组里进行计算,递归的规律刚好是跟更新操作相反。具体代码如下
1
2
3
4
5
6
7
8
9
10
11
|
private int querySum(int index) {
int sum = 0;
for (int i = index; i > 0; i -= lowBit(i)) {
sum += sums[i];
}
return sum;
}
|
例子
算法大部分都有模板代码,树状数组也一样,以下给出一个示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class NumArray {
int[] nums;
int[] sums;
public NumArray(int[] nums) {
this.nums = new int[nums.length];
sums = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
update(i, nums[i]);
}
}
public void update(int index, int val) {
int increaseNum = val - nums[index];
nums[index] = val;
for (int i = index + 1; i < sums.length; i += lowBit(i)) {
sums[i] += increaseNum;
}
}
private int querySum(int index) {
int sum = 0;
for (int i = index; i > 0; i -= lowBit(i)) {
sum += sums[i];
}
return sum;
}
private int lowBit(int n) {
return n & (-n);
}
}
|


